(Part of the work that won the 2023 ACM Gordon Bell Prize, the highest prize in High Performance Computing)
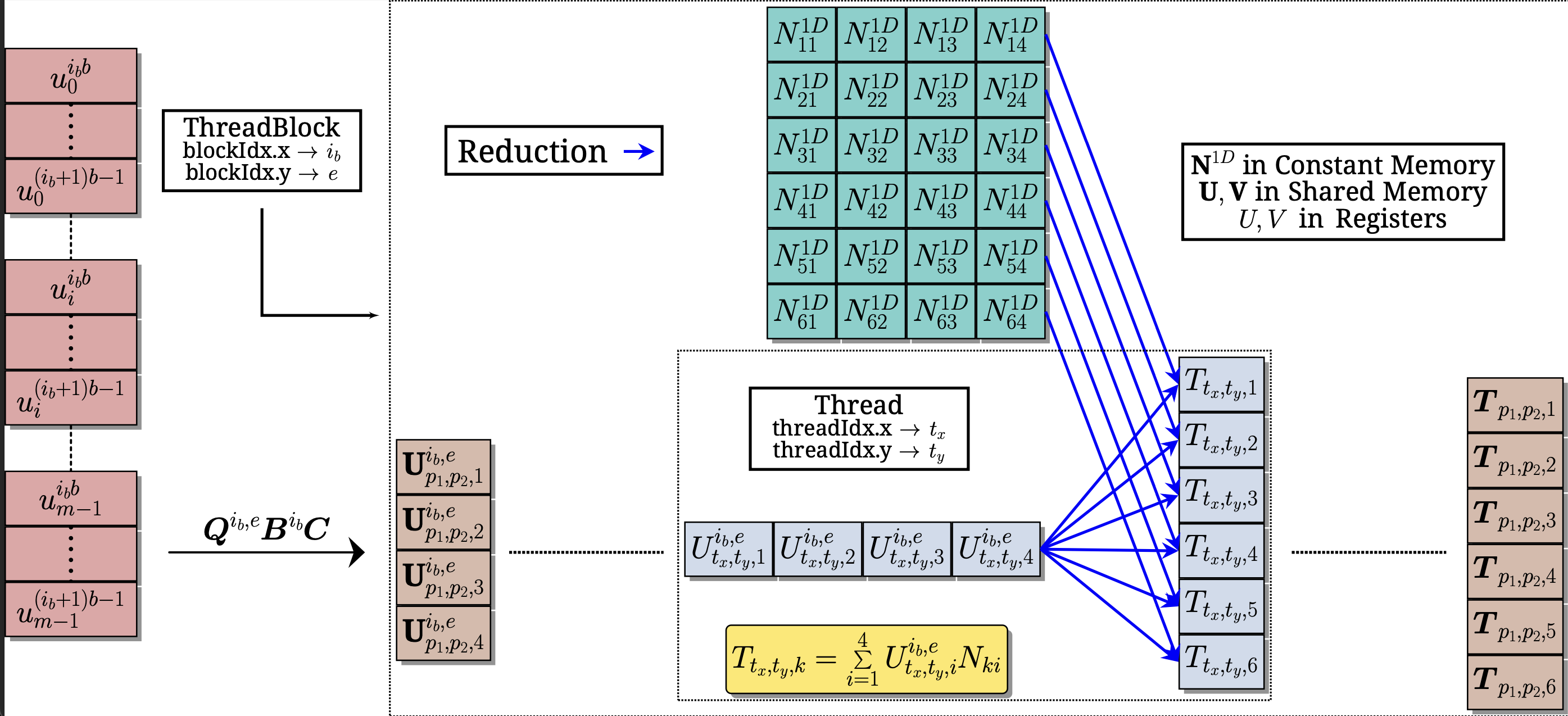
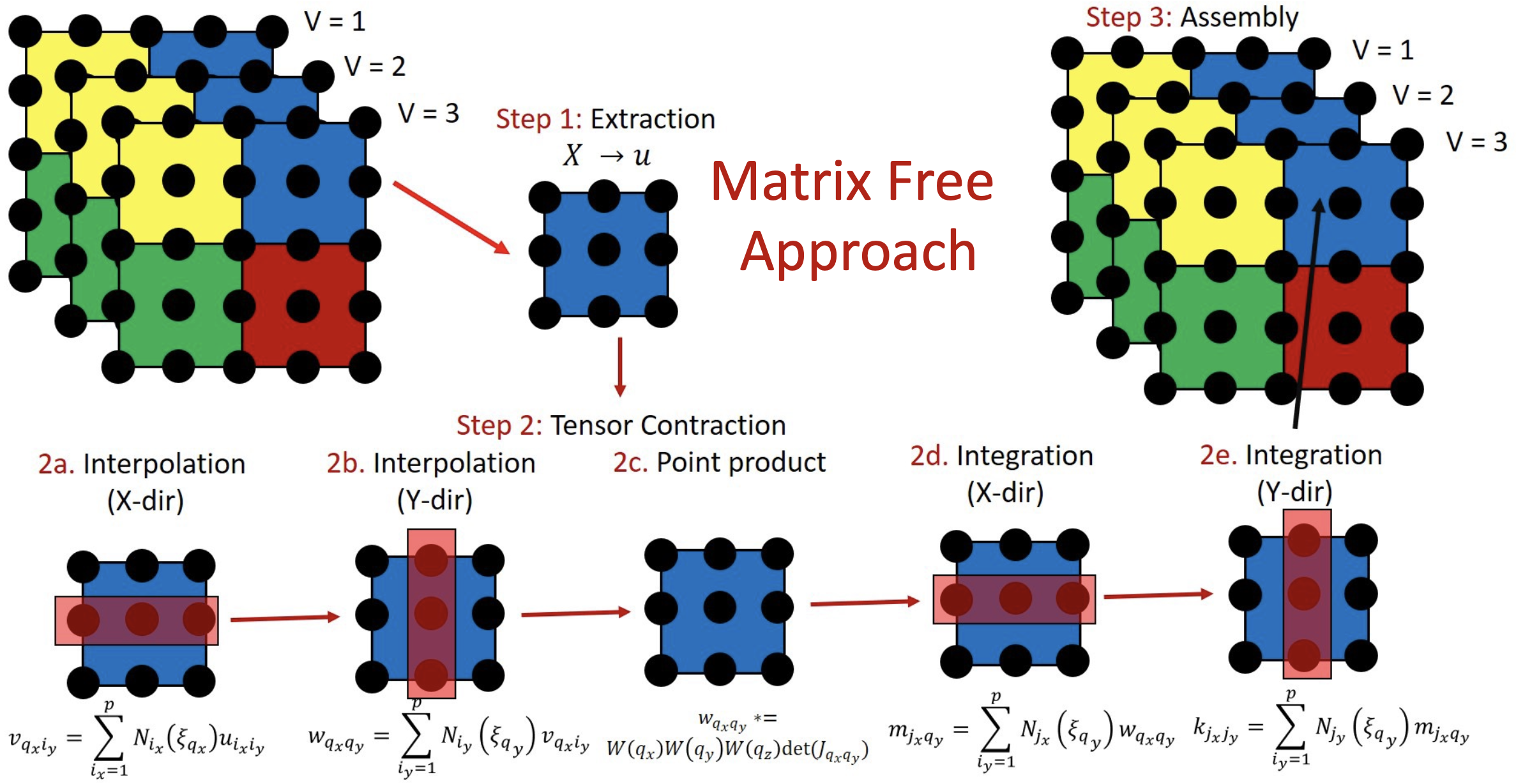
Recent hardware-aware matrix-free algorithms for higher-order finite-element (FE) discretized matrix-vector multiplications reduce floating point operations and data access costs compared to traditional sparse matrix approaches. In this work, we address a critical gap in existing matrix-free implementations which are not well suited for the action of FE discretized matrices on very large number of vectors. In particular, we propose efficient matrix-free algorithms for evaluating FE discretized matrix-multivector products on both multi-node CPU and GPU architectures. To this end, we employ batched evaluation strategies, with the batchsize tailored to underlying hardware architectures, leading to better data locality and enabling further parallelization. On CPUs, we utilize even-odd decomposition, SIMD vectorization, and overlapping computation and communication strategies. On GPUs, we develop strategies to overlap compute with data movement for achieving efficient pipelining and reduced data accesses through the use of GPU-shared memory, constant memory and kernel fusion. Our implementation outperforms the baselines for Helmholtz operator action on 1024 vectors, achieving up to 1.4x improvement on one CPU node and up to 2.8x on one GPU node, while reaching up to 4.4x and 1.5x improvement on multiple nodes for CPUs (3072 cores) and GPUs (24 GPUs), respectively. We further benchmark the performance of the proposed implementation for solving a model eigenvalue problem for 1024 smallest eigenvalue-eigenvector pairs by employing the Chebyshev Filtered Subspace Iteration method, achieving up to 1.5x improvement on one CPU node and up to 2.2x on one GPU node while reaching up to 3.0x and 1.4x improvement on multi-node CPUs (3072 cores) and GPUs (24 GPUs), respectively.
(Winner of the 2023 ACM Gordon Bell Prize, the highest prize in High Performance Computing)
Ab initio electronic-structure has remained dichotomous between achievable accuracy and length-scale. Quantum many-body (QMB) methods realize quantum accuracy but fail to scale. Density functional theory (DFT) scales favorably but remains far from quantum accuracy. We present a framework that breaks this dichotomy by use of three interconnected modules: (i) invDFT: a methodological advance in inverse DFT linking QMB methods to DFT; (ii) MLXC: a machine-learned density functional trained with invDFT data, commensurate with quantum accuracy; (iii) DFT-FE-MLXC: an adaptive higher-order spectral finite-element (FE) based DFT implementation that integrates MLXC with efficient solver strategies and HPC innovations in FE-specific dense linear algebra, mixed-precision algorithms, and asynchronous compute-communication. We demonstrate a paradigm shift in DFT that not only provides an accuracy commensurate with QMB methods in ground-state energies, but also attains an unprecedented performance of 659.7 PFLOPS (43.1% peak FP64 performance) on 619,124 electrons using 8,000 GPU nodes of Frontier supercomputer.